14.1.2. Nonlinear Truss AnalysisΒΆ

  1. The source code is shown below, which can be downloaded here.
  2. Make sure the numpy and matplotlib packages are installed in your Python distribution.
  3. Run the source code in your favorite Python program and should see
../_images/nonlinearTruss.png 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
from openseespy.opensees import *

import numpy as np
import matplotlib.pyplot as plt

# ------------------------------
# Start of model generation
# -----------------------------

# set modelbuilder
wipe()
model('basic', '-ndm', 2, '-ndf', 2)

# variables
A = 4.0
E = 29000.0
alpha = 0.05
sY = 36.0
udisp = 2.5
Nsteps = 1000
Px = 160.0
Py = 0.0

# create nodes
node(1, 0.0, 0.0)
node(2, 72.0, 0.0)
node(3, 168.0, 0.0)
node(4, 48.0, 144.0)

# set boundary condition
fix(1, 1, 1)
fix(2, 1, 1)
fix(3, 1, 1)

# define materials
uniaxialMaterial("Hardening", 1, E, sY, 0.0, alpha/(1-alpha)*E)

# define elements
element("Truss",1,1,4,A,1)
element("Truss",2,2,4,A,1)
element("Truss",3,3,4,A,1)

# create TimeSeries
timeSeries("Linear", 1)

# create a plain load pattern
pattern("Plain", 1, 1)

# Create the nodal load
load(4, Px, Py)

# ------------------------------
# Start of analysis generation
# ------------------------------

# create SOE
system("ProfileSPD")

# create DOF number
numberer("Plain")

# create constraint handler
constraints("Plain")

# create integrator
integrator("LoadControl", 1.0/Nsteps)

# create algorithm
algorithm("Newton")

# create test
test('NormUnbalance',1e-8, 10)

# create analysis object
analysis("Static")

# ------------------------------
# Finally perform the analysis
# ------------------------------

# perform the analysis
data = np.zeros((Nsteps+1,2))
for j in range(Nsteps):
    analyze(1)
    data[j+1,0] = nodeDisp(4,1)
    data[j+1,1] = getLoadFactor(1)*Px

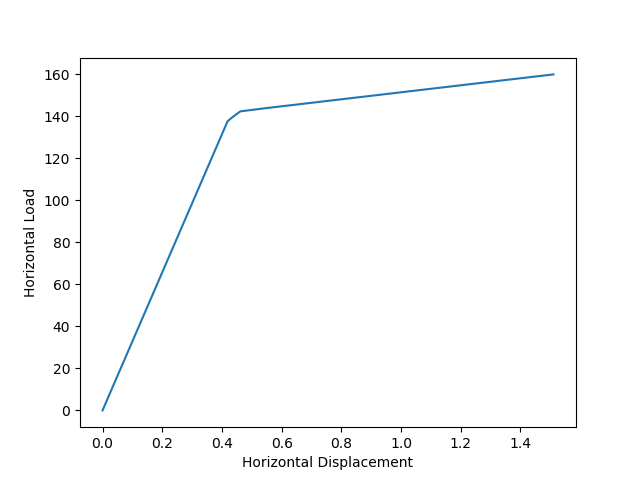
plt.plot(data[:,0], data[:,1])
plt.xlabel('Horizontal Displacement')
plt.ylabel('Horizontal Load')
plt.show()