14.8.2. Two storey steel moment frame with W-sections for displacement-controlled sensitivity analysis¶
The source code is developed by Marin Grubišić at University of Osijek, Croatia.
The numerical model with the associated analysis was described in detail by Prof. Michael Scott in the Portwood Digital blog.
The source code is shown below, which can be downloaded
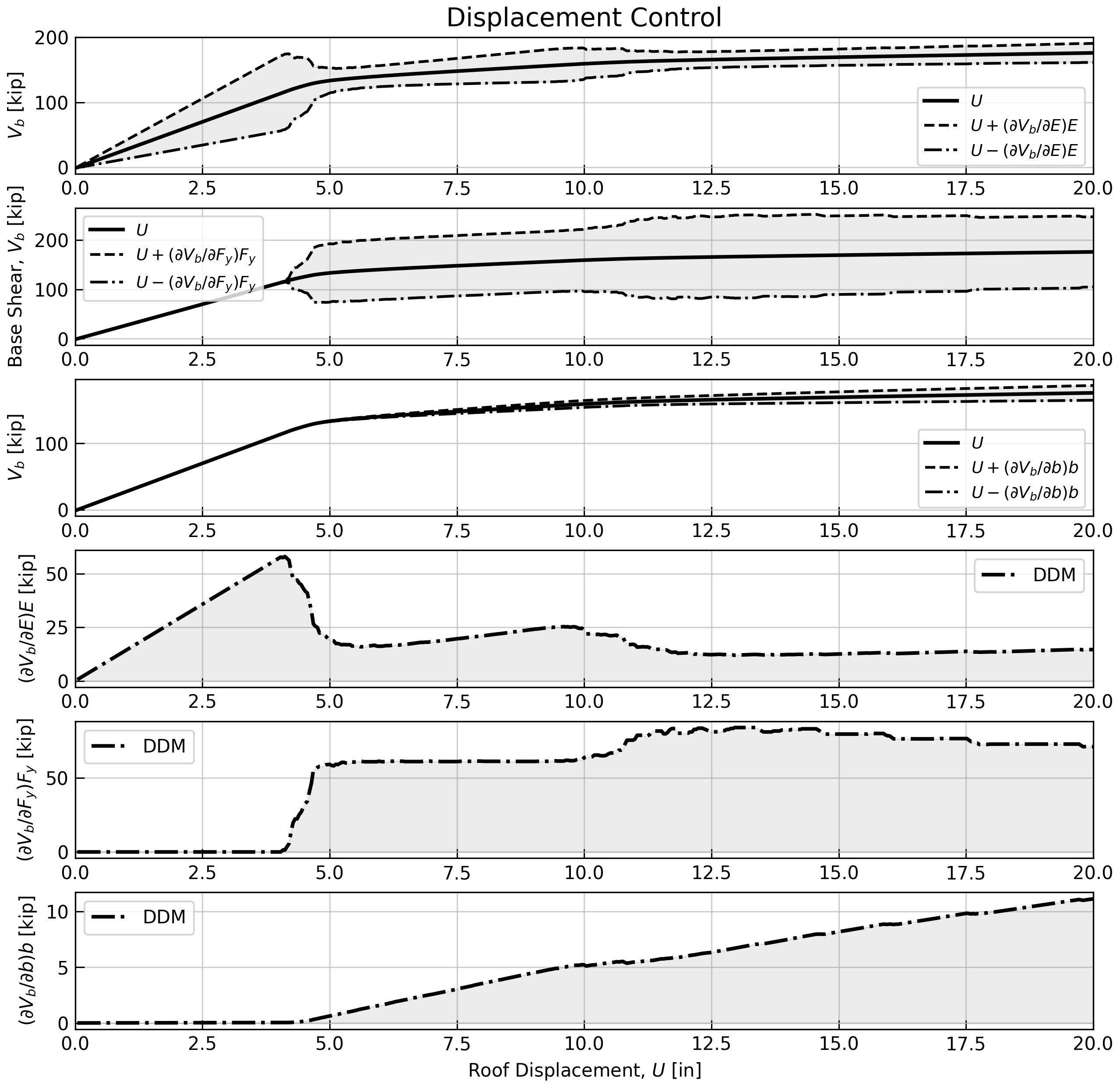
here.Run the source code in your favorite Python program and should see following plot.
1"""
2- The source code is developed by Marin Grubišić https://github.com/mgrubisic
3 at University of Osijek, Croatia.
4- The numerical model with the associated analysis was described in detail by
5 Prof. Michael Scott in the Portwood Digital blog
6 https://portwooddigital.com/2021/01/03/sensitivity-training/
7- Run the source code in your favorite Python program and should see following plot.
8"""
9
10import time
11import sys
12import numpy as np
13import matplotlib.pyplot as plt
14import openseespy.opensees as ops
15
16# +===============================================================================+
17# | OpenSees Header |
18# +===============================================================================+
19nSpaces = 90
20OpenSeesHeader = {"header_00": " ",
21 "header_01": nSpaces * "=",
22 "header_02": "OpenSees -- Open System For Earthquake Engineering Simulation",
23 "header_03": "Pacific Earthquake Engineering Research Center (PEER)",
24 "header_04": "OpenSees " + ops.version() + " 64-Bit",
25 "header_05": "Python " + sys.version,
26 "header_06": " ",
27 "header_07": "(c) Copyright 1999-2021 The Regents of the University of California",
28 "header_08": "All Rights Reserved",
29 "header_09": "(Copyright and Disclaimer @ http://www.berkeley.edu/OpenSees/copyright.html)",
30 "header_10": nSpaces * "=",
31 "header_11": " ",
32 }
33for i in OpenSeesHeader.keys():
34 print(OpenSeesHeader[i].center(nSpaces, " "))
35
36
37def title(title="Title Example", nSpaces=nSpaces):
38 header = (nSpaces-2) * "-"
39 print("+" + header.center((nSpaces-2), " ") + "+")
40 print("|" + title.center((nSpaces-2), " ") + "|")
41 print("+" + header.center((nSpaces-2), " ") + "+")
42
43
44# +===============================================================================+
45# | Units |
46# +===============================================================================+
47inch = 1.0 # define basic units
48kip = 1.0
49sec = 1.0
50
51ft = 12*inch
52lb = kip/1000
53ksi = kip/inch**2
54psf = lb/ft**2
55
56LunitTXT = "inches" # (Length) define basic-unit text for output
57FunitTXT = "kips" # (Force) define basic-unit text for output
58TunitTXT = "seconds" # (Time) define basic-unit text for output
59
60# +===============================================================================+
61# | Define some functions |
62# +===============================================================================+
63
64
65def run_gravity_analysis(steps=10):
66 """
67 Run gravity analysis (in 10 steps)
68 """
69 ops.wipeAnalysis()
70 ops.system("BandGeneral")
71 ops.numberer("RCM")
72 ops.constraints("Transformation")
73 ops.test("NormDispIncr", 1.0E-12, 10, 3)
74 ops.algorithm("Newton") # KrylovNewton
75 ops.integrator("LoadControl", 1/steps)
76 ops.analysis("Static")
77 ops.analyze(steps)
78 title("Gravity Analysis Completed!")
79 # Set the gravity loads to be constant & reset the time in the domain
80 ops.loadConst("-time", 0.0)
81 ops.wipeAnalysis()
82
83
84def run_sensitivity_pushover_analysis(ctrlNode, baseNodes, dof, Dincr, max_disp, SensParam, IOflag=False):
85 """
86 Run pushover analysis with sensitivity
87 """
88 ops.wipeAnalysis()
89 start_time = time.time()
90 ops.loadConst("-time", 0.0)
91
92 title("Running Displacement-Control Pushover Sensitivity Analysis ...")
93
94 testType = "NormDispIncr" # EnergyIncr
95 tolInit = 1.0E-8
96 iterInit = 10 # Set the initial Max Number of Iterations
97 algorithmType = "Newton" # Set the algorithm type
98
99 ops.system("BandGeneral")
100 ops.constraints("Transformation")
101 ops.numberer("RCM")
102 ops.test(testType, tolInit, iterInit)
103 ops.algorithm(algorithmType)
104 # Change the integration scheme to be displacement control
105 # node dof init Jd min max
106 ops.integrator("DisplacementControl", ctrlNode, dof, Dincr)
107 ops.analysis("Static")
108 ops.sensitivityAlgorithm("-computeAtEachStep") # automatically compute sensitivity at the end of each step
109
110 if IOflag:
111 print(f"Single Pushover: Push node {ctrlNode} to {max_disp} {LunitTXT}.\n")
112
113 # Set some parameters
114 tCurrent = ops.getTime()
115 currentStep = 1
116
117 outputs = {"time": np.array([]),
118 "disp": np.array([]),
119 "force": np.array([]),
120 }
121
122 for sens in SensParam:
123 outputs[f"sensLambda_{sens}"] = np.array([]),
124
125 nodeList = []
126 for node in baseNodes:
127 nodeList.append(f"- ops.nodeReaction({node}, dof) ")
128
129 nodeList = "".join(nodeList)
130 currentDisp = ops.nodeDisp(ctrlNode, dof)
131 ok = 0
132
133 while ok == 0 and currentDisp < max_disp:
134 ops.reactions()
135 ok = ops.analyze(1)
136 tCurrent = ops.getTime()
137 currentDisp = ops.nodeDisp(ctrlNode, dof)
138
139 if IOflag:
140 print(f"Current displacement ==> {ops.nodeDisp(ctrlNode, dof):.3f} {LunitTXT}")
141
142 # if the analysis fails try initial tangent iteration
143 if ok != 0:
144 print("\n==> Trying relaxed convergence...")
145 ops.test(testType, tolInit/0.01, iterInit*50)
146 ok = ops.analyze(1)
147 if ok == 0:
148 print("==> that worked ... back to default analysis...\n")
149 ops.test(testType, tolInit, iterInit)
150
151 if ok != 0:
152 print("\n==> Trying Newton with initial then current...")
153 ops.test(testType, tolInit/0.01, iterInit*50)
154 ops.algorithm("Newton", "-initialThenCurrent")
155 ok = ops.analyze(1)
156 if ok == 0:
157 print("==> that worked ... back to default analysis...\n")
158 ops.algorithm(algorithmType)
159 ops.test(testType, tolInit, iterInit)
160
161 if ok != 0:
162 print("\n==> Trying ModifiedNewton with initial...")
163 ops.test(testType, tolInit/0.01, iterInit*50)
164 ops.algorithm("ModifiedNewton", "-initial")
165 ok = ops.analyze(1)
166 if ok == 0:
167 print("==> that worked ... back to default analysis...\n")
168 ops.algorithm(algorithmType)
169 ops.test(testType, tolInit, iterInit)
170
171 currentStep += 1
172 tCurrent = ops.getTime()
173
174 outputs["time"] = np.append(outputs["time"], tCurrent)
175 outputs["disp"] = np.append(outputs["disp"], ops.nodeDisp(ctrlNode, dof))
176 outputs["force"] = np.append(outputs["force"], eval(nodeList))
177
178 for sens in SensParam:
179 # sensLambda(patternTag, paramTag)
180 outputs[f"sensLambda_{sens}"] = np.append(outputs[f"sensLambda_{sens}"], ops.sensLambda(1, sens))
181
182 # Print a message to indicate if analysis completed succesfully or not
183 if ok == 0:
184 title("Pushover Analysis Completed Successfully!")
185 else:
186 title("Pushover Analysis Completed Failed!")
187
188 print(f"Analysis elapsed time is {(time.time() - start_time):.3f} seconds.\n")
189
190 return outputs
191
192
193# +===============================================================================+
194# | Define model |
195# +===============================================================================+
196# Create ModelBuilder
197# -------------------
198ops.wipe()
199ops.model("basic", "-ndm", 2, "-ndf", 3)
200
201# Create nodes
202# ------------
203ops.node(1, 0.0, 0.0) # Ground Level
204ops.node(2, 30*ft, 0.0)
205ops.node(3, 0.0, 15*ft) # 1st Floor Level
206ops.node(4, 30*ft, 15*ft)
207ops.node(5, 0.0, 2*15*ft) # 2nd Floor Level
208ops.node(6, 30*ft, 2*15*ft)
209
210# Fix supports at base of columns
211# -------------------------------
212ops.fix(1, 1, 1, 1)
213ops.fix(2, 1, 1, 1)
214
215# Define material
216# ---------------
217matTag = 1
218Fy = 50.0*ksi # Yield stress
219Es = 29000.0*ksi # Modulus of Elasticity of Steel
220b = 1/100 # 1% Strain hardening ratio
221
222# Sensitivity-ready steel materials: Hardening, Steel01, SteelMP, BoucWen, SteelBRB, StainlessECThermal, SteelECThermal, ...
223ops.uniaxialMaterial("Steel01", matTag, Fy, Es, b)
224# ops.uniaxialMaterial("SteelMP", matTag, Fy, Es, b)
225
226# Define sections
227# ---------------
228# Sections defined with "canned" section ("WFSection2d"), otherwise use a FiberSection object (ops.section("Fiber",...))
229colSecTag, beamSecTag = 1, 2
230WSection = {"W18x76": [18.2*inch, 0.425*inch, 11.04*inch, 0.68*inch], # [d, tw, bf, tf]
231 "W14X90": [14.02*inch, 0.44*inch, 14.52*inch, 0.71*inch], # [d, tw, bf, tf]
232 }
233
234# secTag, matTag, [d, tw, bf, tf], Nfw, Nff
235ops.section("WFSection2d", colSecTag, matTag, *WSection["W14X90"], 20, 4) # Column section
236ops.section("WFSection2d", beamSecTag, matTag, *WSection["W18x76"], 20, 4) # Beam section
237
238# Define elements
239# ---------------
240colTransTag, beamTransTag = 1, 2
241# Linear, PDelta, Corotational
242ops.geomTransf("Corotational", colTransTag)
243ops.geomTransf("Linear", beamTransTag)
244
245colIntTag, beamIntTag = 1, 2
246nip = 5
247# Lobatto, Legendre, NewtonCotes, Radau, Trapezoidal, CompositeSimpson
248ops.beamIntegration("Lobatto", colIntTag, colSecTag, nip),
249ops.beamIntegration("Lobatto", beamIntTag, beamSecTag, nip)
250
251# Column elements
252ops.element("forceBeamColumn", 10, 1, 3, colTransTag, colIntTag, "-mass", 0.0)
253ops.element("forceBeamColumn", 11, 3, 5, colTransTag, colIntTag, "-mass", 0.0)
254ops.element("forceBeamColumn", 12, 2, 4, colTransTag, colIntTag, "-mass", 0.0)
255ops.element("forceBeamColumn", 13, 4, 6, colTransTag, colIntTag, "-mass", 0.0)
256
257# Beam elements
258ops.element("forceBeamColumn", 14, 3, 4, beamTransTag, beamIntTag, "-mass", 0.0)
259ops.element("forceBeamColumn", 15, 5, 6, beamTransTag, beamIntTag, "-mass", 0.0)
260
261# Create a Plain load pattern with a Linear TimeSeries
262# ----------------------------------------------------
263ops.timeSeries("Linear", 1)
264ops.pattern("Plain", 1, 1)
265
266# +===============================================================================+
267# | Define Sensitivity Parameters |
268# +===============================================================================+
269# /// Each parameter must be unique in the FE domain, and all parameter tags MUST be numbered sequentially starting from 1! ///
270ops.parameter(1) # Blank parameters
271ops.parameter(2)
272ops.parameter(3)
273for ele in [10, 11, 12, 13]: # Only column elements
274 ops.addToParameter(1, "element", ele, "E") # "E"
275 # Check the sensitivity parameter name in *.cpp files ("sigmaY" or "fy", somewhere also "Fy")
276 # https://github.com/OpenSees/OpenSees/blob/master/SRC/material/uniaxial/Steel02.cpp
277 ops.addToParameter(2, "element", ele, "fy") # "sigmaY" or "fy" or "Fy"
278 ops.addToParameter(3, "element", ele, "b") # "b"
279
280title("Model Built")
281
282# Run analysis with 10 steps
283# -------------------------
284run_gravity_analysis(steps=10)
285
286# +===============================================================================+
287# | Define nodal loads & Run the analysis |
288# +===============================================================================+
289# Create nodal loads at nodes 3 & 5
290# nd FX FY MZ
291ops.load(3, 1/3, 0.0, 0.0)
292ops.load(5, 2/3, 0.0, 0.0)
293
294max_disp = 20*inch
295pushover_output = run_sensitivity_pushover_analysis(
296 ctrlNode=5, baseNodes=[1, 2], dof=1, Dincr=(1/25)*inch, max_disp=max_disp, SensParam=ops.getParamTags(), IOflag=False)
297
298# +===============================================================================+
299# | Plot results |
300# +===============================================================================+
301rows, columns = len(ops.getParamTags())*2, 1
302grid = plt.GridSpec(rows, columns, wspace=0.25, hspace=0.25)
303fig = plt.figure(figsize=(10, 10))
304
305ParamSym = ["E", "F_y", "b"]
306ParamVars = [Es, Fy, b]
307
308
309def plot_params():
310 plt.rcParams['axes.axisbelow'] = True
311 plt.xlim(xmin=0.0, xmax=max_disp)
312 plt.grid(True, color="silver", linestyle="solid", linewidth=0.75, alpha=0.75)
313 plt.tick_params(direction="in", length=5, colors="k", width=0.75)
314
315
316for s in range(0, rows):
317 # Create subplots
318 # ---------------
319 if s < 3:
320 plt.subplot(grid[s]), plot_params()
321 plt.plot(pushover_output["disp"], pushover_output["force"], "-k", linewidth=2.0, label="$U$")
322 plt.plot(pushover_output["disp"], pushover_output["force"] +
323 pushover_output[f"sensLambda_{s+1}"] * ParamVars[s], "--k", linewidth=1.5, label=f"$U + (\partial V_b/\partial {ParamSym[s]}){ParamSym[s]}$")
324 plt.plot(pushover_output["disp"], pushover_output["force"] -
325 pushover_output[f"sensLambda_{s+1}"] * ParamVars[s], "-.k", linewidth=1.5, label=f"$U - (\partial V_b/\partial {ParamSym[s]}){ParamSym[s]}$")
326 plt.fill_between(pushover_output["disp"], pushover_output["force"] +
327 pushover_output[f"sensLambda_{s+1}"] * ParamVars[s], pushover_output["force"] - pushover_output[f"sensLambda_{s+1}"] * ParamVars[s], color='grey', alpha=0.15)
328 plt.ylabel(r"$V_b$ [kip]")
329 if s == 0:
330 plt.title(r"Displacement Control", fontsize=14)
331 if s == 1:
332 plt.ylabel(r"Base Shear, $V_b$ [kip]")
333 plt.legend(fontsize=9)
334
335 if s >= 3:
336 plt.subplot(grid[s]), plot_params()
337 plt.plot(pushover_output["disp"],
338 pushover_output[f"sensLambda_{s-2}"] * ParamVars[s-3], "-.k", linewidth=2.0, label="DDM")
339 plt.fill_between(pushover_output["disp"],
340 pushover_output[f"sensLambda_{s-2}"] * ParamVars[s-3], color='grey', alpha=0.15)
341 plt.ylabel(f"$(\partial V_b/\partial {ParamSym[s-3]}){ParamSym[s-3]}$ [kip]")
342 if s == 5:
343 plt.xlabel(r"Roof Displacement, $U$ [in]")
344 plt.legend()
345
346 s += 1
347
348# Save figure
349# -----------
350plt.savefig("SteelFrameSensitivity2D_v1.png", bbox_inches="tight", pad_inches=0.05, dpi=300, format="png")
351plt.show()