14.8.1. Simple cantilever for load-controlled sensitivity analysis¶
The source code is developed by Marin Grubišić at University of Osijek, Croatia.
The numerical model with the associated analysis was described in detail by Prof. Michael Scott within OpenSees Days 2011.
The source code is shown below, which can be downloaded
here.Run the source code in your favorite Python program and should see following plot.
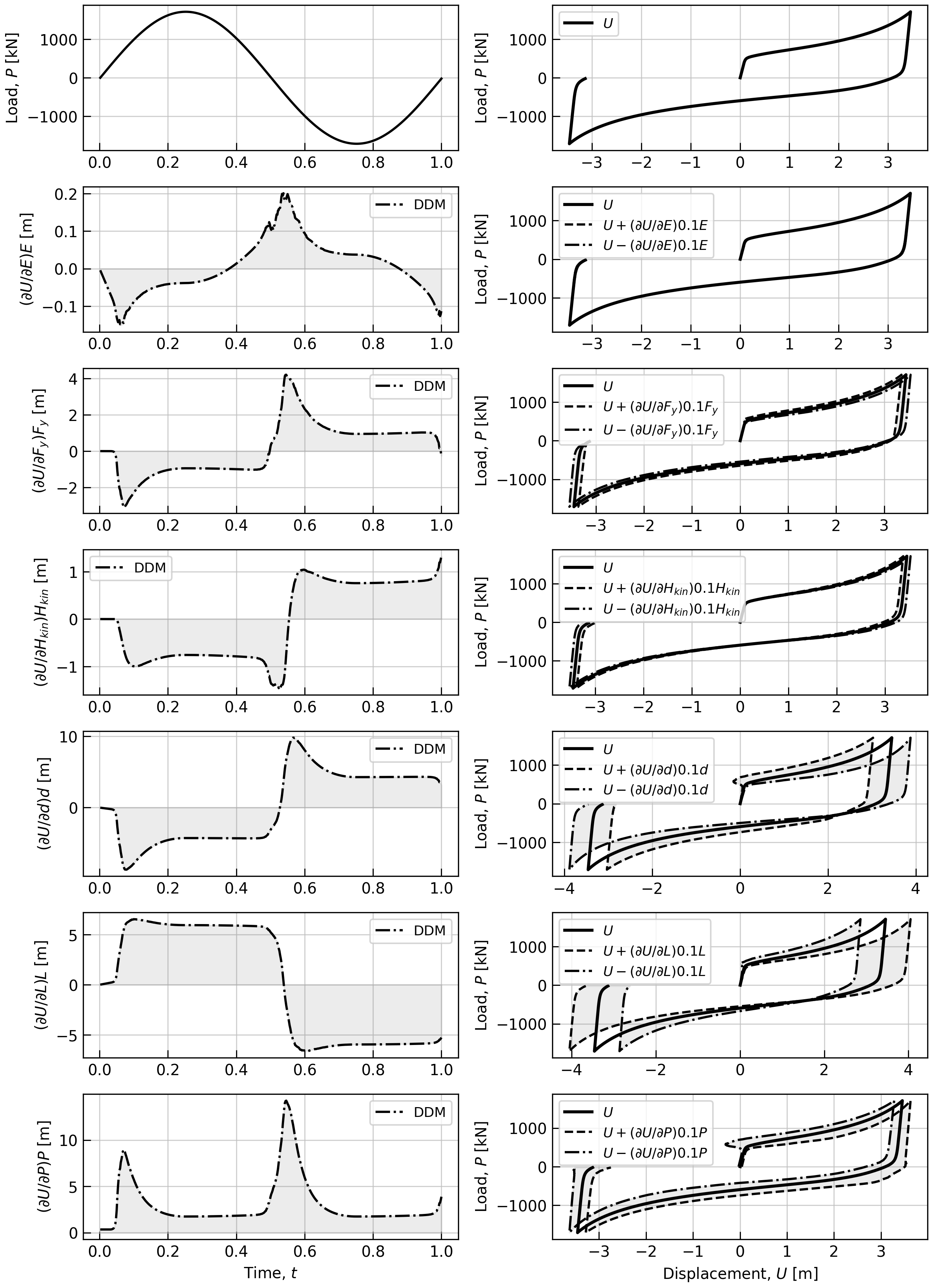
1"""
2- The source code is developed by Marin Grubišić https://github.com/mgrubisic
3 at University of Osijek, Croatia.
4- The numerical model with the associated analysis was described in detail by
5 Prof. Michael Scott within OpenSees Days 2011
6 https://opensees.berkeley.edu/OpenSees/workshops/OpenSeesDays2011/B5_MHS.pdf
7- Run the source code in your favorite Python program and should see following plot.
8"""
9
10import time
11import sys
12import numpy as np
13import matplotlib.pyplot as plt
14import openseespy.opensees as ops
15
16# +===============================================================================+
17# | OpenSees Header |
18# +===============================================================================+
19nSpaces = 90
20OpenSeesHeader = {"header_00": " ",
21 "header_01": nSpaces * "=",
22 "header_02": "OpenSees -- Open System For Earthquake Engineering Simulation",
23 "header_03": "Pacific Earthquake Engineering Research Center (PEER)",
24 "header_04": "OpenSees " + ops.version() + " 64-Bit",
25 "header_05": "Python " + sys.version,
26 "header_06": " ",
27 "header_07": "(c) Copyright 1999-2021 The Regents of the University of California",
28 "header_08": "All Rights Reserved",
29 "header_09": "(Copyright and Disclaimer @ http://www.berkeley.edu/OpenSees/copyright.html)",
30 "header_10": nSpaces * "=",
31 "header_11": " ",
32 }
33for i in OpenSeesHeader.keys():
34 print(OpenSeesHeader[i].center(nSpaces, " "))
35
36
37def title(title="Title Example", nSpaces=nSpaces):
38 header = (nSpaces-2) * "-"
39 print("+" + header.center((nSpaces-2), " ") + "+")
40 print("|" + title.center((nSpaces-2), " ") + "|")
41 print("+" + header.center((nSpaces-2), " ") + "+")
42
43
44# +===============================================================================+
45# | Units |
46# +===============================================================================+
47m, kN, sec = 1.0, 1.0, 1.0 # meter for length, kilonewton for force, second for time
48
49# Angle
50rad = 1.0
51deg = np.pi/180.0*rad
52
53# Length, Area, Volume, Second moment of area
54m2, m3, m4 = m**2, m**3, m**4
55cm, cm2, cm3, cm4 = m*1E-2, m*1E-4, m*1E-6, m*1E-8
56mm, mm2, mm3, mm4 = m*1E-3, m*1E-6, m*1E-9, m*1E-12
57inch = 0.0254*m
58ft = 0.3048*m
59
60# Force
61N = kN*1E-3
62g = 9.80665*m/(sec**2)
63
64# Mass
65kg = N*sec**2/m
66ton = kg*1E3
67lbs = 0.45359237*kg
68kip = 453.59237*kg
69
70# Pressure
71Pa, kPa, MPa, GPa = N/m**2, 1E3*N/m**2, 1E6*N/m**2, 1E9*N/m**2
72pcf = lbs/(ft**3)
73ksi = kip/(inch**2)
74psi = ksi/1E3
75
76Inf = 1.0E12 # a really large number
77Null = 1/Inf # a really small number
78
79LunitTXT = "m" # (Length) define basic-unit text for output
80FunitTXT = "kN" # (Force) define basic-unit text for output
81TunitTXT = "seconds" # (Time) define basic-unit text for output
82
83# +===============================================================================+
84# | Define some functions |
85# +===============================================================================+
86
87
88def run_sensitivity_analysis(ctrlNode, dof, baseNode, SensParam, steps=500, IOflag=False):
89 """
90 Run load-control sensitivity analysis
91 """
92 ops.wipeAnalysis()
93 start_time = time.time()
94
95 title("Running Load-Control Sensitivity Analysis ...")
96
97 ops.system("BandGeneral")
98 ops.numberer("RCM")
99 ops.constraints("Transformation")
100 ops.test("NormDispIncr", 1.0E-12, 10, 3)
101 ops.algorithm("Newton") # KrylovNewton
102 ops.integrator("LoadControl", 1/steps)
103 ops.analysis("Static")
104 ops.sensitivityAlgorithm("-computeAtEachStep") # automatically compute sensitivity at the end of each step
105
106 outputs = {"time": np.array([]),
107 "disp": np.array([]),
108 "force": np.array([]),
109 }
110
111 for sens in SensParam:
112 outputs[f"sensDisp_{sens}"] = np.array([]),
113
114 for i in range(steps):
115 ops.reactions()
116 if IOflag:
117 print(
118 f"Single Cycle Response: Step #{i}, Node #{ctrlNode}: {ops.nodeDisp(ctrlNode, dof):.3f} {LunitTXT} / {-ops.nodeReaction(baseNode, dof):.2f} {FunitTXT}.")
119 ops.analyze(1)
120 tCurrent = ops.getTime()
121
122 outputs["time"] = np.append(outputs["time"], tCurrent)
123 outputs["disp"] = np.append(outputs["disp"], ops.nodeDisp(ctrlNode, dof))
124 outputs["force"] = np.append(outputs["force"], -ops.nodeReaction(baseNode, dof))
125
126 for sens in SensParam:
127 # sensDisp(patternTag, paramTag)
128 outputs[f"sensDisp_{sens}"] = np.append(outputs[f"sensDisp_{sens}"], ops.sensNodeDisp(ctrlNode, dof, sens))
129
130 title("Sensitvity Analysis Completed!")
131 print(f"Analysis elapsed time is {(time.time() - start_time):.3f} seconds.\n")
132
133 return outputs
134
135
136# +===============================================================================+
137# | Define model |
138# +===============================================================================+
139# Create ModelBuilder
140# -------------------
141ops.wipe()
142ops.model("basic", "-ndm", 2, "-ndf", 3)
143
144# Create nodes
145# ------------
146L = 5*m
147ops.node(1, 0.0, 0.0) # Fixed end
148ops.node(2, L, 0.0) # Free end
149
150# Fixed support
151# -------------
152ops.fix(1, 1, 1, 1)
153
154# Define material
155# ---------------
156matTag = 1
157Fy = 410*MPa # Yield stress
158Es = 200*GPa # Modulus of Elasticity of Steel
159b = 2/100 # 2% Strain hardening ratio
160Hkin = b/(1-b)*Es
161
162# Sensitivity-ready steel materials: Hardening, Steel01, SteelMP, BoucWen, SteelBRB, StainlessECThermal, SteelECThermal, ...
163# Hardening Sensitivity Params: sigmaY/fy/Fy, E, H_kin/Hkin, H_iso/Hiso
164ops.uniaxialMaterial("Hardening", matTag, Es, Fy, 0, Hkin)
165
166# ops.uniaxialMaterial("Steel01", matTag, Fy, Es, b) # Sensitivity Params: sigmaY/fy/Fy, E, b, a1, a2, a3, a4
167# ops.uniaxialMaterial("SteelMP", matTag, Fy, Es, b) # Sensitivity Params: sigmaY/fy, E, b
168
169# Define sections
170# ---------------
171# Sections defined with "canned" section ("WFSection2d"), otherwise use a FiberSection object (ops.section("Fiber",...))
172beamSecTag = 1
173beamWidth, beamDepth = 10*cm, 50*cm
174# secTag, matTag, d, tw, bf, tf, Nfw, Nff
175ops.section("WFSection2d", beamSecTag, matTag, beamDepth, beamWidth, beamWidth, 0, 20, 0) # Beam section
176
177# Define elements
178# ---------------
179beamTransTag, beamIntTag = 1, 1
180# Linear, PDelta, Corotational
181ops.geomTransf("Corotational", beamTransTag)
182
183nip = 5
184# Lobatto, Legendre, NewtonCotes, Radau, Trapezoidal, CompositeSimpson
185ops.beamIntegration("Legendre", beamIntTag, beamSecTag, nip)
186
187# Beam elements
188numEle = 5
189meshSize = L/numEle # mesh size
190
191eleType = "dispBeamColumn" # forceBeamColumn, "dispBeamColumn"
192# tag, Npts, nodes, type, dofs, size, eleType, transfTag, beamIntTag
193ops.mesh("line", 1, 2, *[1, 2], 0, 3, meshSize, eleType, beamTransTag, beamIntTag)
194
195# Create a Plain load pattern with a Sine/Trig TimeSeries
196# -------------------------------------------------------
197# tag, tStart, tEnd, period, factor
198ops.timeSeries("Trig", 1, 0.0, 1.0, 1.0, "-factor", 1.0) # "Sine", "Trig" or "Triangle"
199ops.pattern("Plain", 1, 1)
200
201P = 1710*kN
202# Create nodal loads at node 2
203# nd FX FY MZ
204ops.load(2, 0.0, P, 0.0)
205
206# +===============================================================================+
207# | Define Sensitivity Parameters |
208# +===============================================================================+
209# /// Each parameter must be unique in the FE domain, and all parameter tags MUST be numbered sequentially starting from 1! ///
210ops.parameter(1) # Blank parameters
211ops.parameter(2)
212ops.parameter(3)
213ops.parameter(4)
214for ele in range(1, numEle+1): # Only column elements
215 ops.addToParameter(1, "element", ele, "E") # E
216 # Check the sensitivity parameter names in *.cpp files ("sigmaY" or "fy" or "Fy")
217 # https://github.com/OpenSees/OpenSees/blob/master/SRC/material/uniaxial/HardeningMaterial.cpp
218 ops.addToParameter(2, "element", ele, "Fy") # "sigmaY" or "fy" or "Fy"
219 ops.addToParameter(3, "element", ele, "Hkin") # "H_kin" or "Hkin" or "b"
220 ops.addToParameter(4, "element", ele, "d") # "d"
221
222ops.parameter(5, "node", 2, "coord", 1) # parameter for coordinate of node 2 in DOF "1" (PX=1, PY=2, MZ=3)
223# Map parameter 6 to vertical load at node 2 contained in load pattern 1 (last argument is global DOF, e.g., in 2D PX=1, PY=2, MZ=3)
224ops.parameter(6, "loadPattern", 1, "loadAtNode", 2, 2)
225
226ParamSym = ["E", "F_y", "H_{kin}", "d", "L", "P"]
227ParamVars = [Es, Fy, Hkin, beamDepth, L, P]
228
229title("Model Built")
230
231# +===============================================================================+
232# | Run the analysis |
233# +===============================================================================+
234# Run analysis with 500 steps
235# -------------------------
236outputs = run_sensitivity_analysis(
237 ctrlNode=2, dof=2, baseNode=1, SensParam=ops.getParamTags(), steps=500, IOflag=False)
238
239# +===============================================================================+
240# | Plot results |
241# +===============================================================================+
242rows, columns = 7, 2
243grid = plt.GridSpec(rows, columns, wspace=0.25, hspace=0.25)
244plt.figure(figsize=(10, 15))
245
246
247def plot_params():
248 plt.rc("axes", axisbelow=True)
249 plt.tick_params(direction="in", length=5, colors="k", width=0.75)
250 plt.grid(True, color="silver", linestyle="solid",
251 linewidth=0.75, alpha=0.75)
252
253
254# Subplot #1
255# ----------
256plt.subplot(grid[0]), plot_params()
257plt.plot(outputs["time"],
258 outputs["force"], "-k", linewidth=1.5)
259plt.ylabel(r"Load, $P$ [kN]")
260
261# Subplot #2
262# ----------
263plt.subplot(grid[1]), plot_params()
264plt.plot(outputs["disp"],
265 outputs["force"], "-k", linewidth=2.0, label="$U$")
266plt.ylabel(r"Load, $P$ [kN]"), plt.legend(fontsize=9)
267
268i, j = 2, 0
269for p in ParamVars:
270 # Subplot #i
271 # ----------
272 plt.subplot(grid[i]), plot_params()
273 plt.plot(outputs["time"], outputs[f"sensDisp_{j+1}"]*p, "-.k", linewidth=1.5, label="DDM")
274 plt.fill_between(outputs["time"], outputs[f"sensDisp_{j+1}"]*p, color='grey', alpha=0.15)
275 plt.ylabel(f"$(\partial U/\partial {ParamSym[j]}){ParamSym[j]}$ [m]")
276 plt.legend(fontsize=9)
277 if j == 5:
278 plt.xlabel(r"Time, $t$")
279
280 # Subplot #ii
281 # -----------
282 plt.subplot(grid[i+1]), plot_params()
283 plt.plot(outputs["disp"], outputs["force"], "-k", linewidth=2.0, label="$U$")
284 plt.plot(outputs["disp"] + outputs[f"sensDisp_{j+1}"] * 0.1*p,
285 outputs["force"], "--k", linewidth=1.5, label=f"$U + (\partial U/\partial {ParamSym[j]})0.1{ParamSym[j]}$")
286 plt.plot(outputs["disp"] - outputs[f"sensDisp_{j+1}"] * 0.1*p,
287 outputs["force"], "-.k", linewidth=1.5, label=f"$U - (\partial U/\partial {ParamSym[j]})0.1{ParamSym[j]}$")
288
289 plt.fill_betweenx(outputs["force"], outputs["disp"] +
290 outputs[f"sensDisp_{j+1}"] * 0.1*p, outputs["disp"] - outputs[f"sensDisp_{j+1}"] * 0.1*p, color='grey', alpha=0.15)
291
292 plt.ylabel(r"Load, $P$ [kN]")
293 plt.legend(fontsize=9)
294 if j == 5:
295 plt.xlabel(r"Displacement, $U$ [m]")
296 i += 2
297 j += 1
298
299
300# Save figure
301# -----------
302plt.savefig("CantileverSensitivity2D_v1.png", bbox_inches="tight", pad_inches=0.05, dpi=300, format="png")
303plt.show()